Düzen Kuşağı..............Çalışmalarına Katılmak İçin Tıklayınız..

Doğadaki Mükemmel Tasarımlar Arı Peteği ve Altıgen  (Beyin Fırtınası İle Düzen Kuşağında İşlenebilecek Güzel Bir Konu) 1- Önce tahtaya her kenarı eşit olan bir altıgen çizilir 2- Altıgenin değişkenliği olmayan bir şekil olduğunu kim ispatlayabilir diye sorulur 3- Gelen cevaplarla köşeler birleştirildiğinde altıgenin içinde altı tane değişkenliği olmayan eşkenar üçgenin çıktığı görülür. Ve bütüne giderken bu değişkenliği olmayan şeklinde kullanılabileceği söylenir 4- Doğada altıgenin nerede olabileceği sorulur 5- Arı peteği cevabı alındıktan sonra neden arı, peteğini altıgen yapmış olabilir diye sorulur. 6- Boşluk olmadığı cevabı geldikten sonra; bu yüzden fazla bal alır mı? sorusu sorulur. 7- Peki biz hangi eşyalarımızda bu şekli kullanabiliriz sorusundan sonra muhtemelen şu cevaplar  gelecektir.

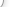	Kuranda Arı 16:68 - Senin Rabbin bal arısına şöyle vahyetti: Dağlardan, ağaçlardan ve insanların kuracakları kovanlardan kendine evler edin. 16:69 - Sonra meyvaların hepsinden ye de, Rabbinin (sana) kolay kıldığı yollara gir, diye ilham etti. Onların karınlarından renkleri çeşitli bir bal çıkar ki, onda insanlar için şifâ vardır. Şüphesiz ki bunda düşünen bir millet için, büyük bir ibret vardır.

Bal arıları milyonlarca yıldır peteklerini altıgen yapmaktadır (On milyonlarca yıl öncesine ait arı fosillerinden bu anlaşılmaktadır) Acaba neden bu şekil dikdörtgen, beşgen, sekizgen değil de altıgendir? Bunu araştıran matematikçiler birim alanın tamamen kullanılması ve en az malzemeyle petek yapılabilmesi için en ideal şeklin altıgen olduğunu ortaya koydular Petekler üçgen ya da dörtgen olsaydı, boşluksuz kullanılabilecekti Fakat altıgen hücreler için kullanılan malzeme üçgen ya da dörtgen için kullanılan malzemeden daha azdır Diğer birçok geometrik şekilde ise kullanılmayan bölgeler ortaya çıkacaktı Sonuç olarak altıgen hücre, en çok miktarda bal depolarken, yapılması için en az balmumu gereken şekildir
Dişi (işçi) arıların bu çalışmalarında en çok ilgi çeken durumlardan biri onbinlerce işçi arının her birinin, birer tuğlacığını bıraktığı bu yapının, geometrik ölçülere bütünüyle uyabilmesidir Matematikçiler verilen belirli miktardaki balmumuyla yumurtadan çıkacak kurtçukları içine alabilecek daha geniş bir yer yapılamayacağını ispatlamışlardırBöylece işçi arılar belirli miktardaki gereçle, gereken büyüklükteki bir yapının en ekonomik biçimde nasıl yapılabileceğini göstermektedirler
Antoine Ferchault adındaki bir Fransız böcek bilgini, bunu “Arılar problemi” diye tanınan bir geometri problemi olarak ortaya koymuştur Bu problem şudur: “Tabanı birbirlerine göre eğimi aynı olan üç çeşit eşkenar dörtgen ile kapanmış düzgün altıgen bir dik prizma verilsin Bu prizmanın toplam yüzey alanının en küçük değerde olması için eşkenar dörtgenler arasındaki açılar ne olmalıdır?” Biri Alman, biri İsviçreli, biri de İngiliz olan üç tanınmış matematikçi bu problemin çözümüyle uğraştılar ve şu sonuca vardılar: 70° 32′ (70 derece ve 32 dakika) Gerçekten de bu, dişi bal arılarının yaptığı petek gözeneklerinin açısının tamı t----- aynısıdır
İşçi arılarımız peteğin yapımına birkaç farklı noktadan başlarlar İş ilerledikçe peteğin gözenekleri orta yerde birleşir Bu durumda kaynaşma noktasındaki peteklerin açıları yine kusursuzdur Bu işçi arıların peteğin yapımına rastgele koyulmadıklarını, başlangıç ve bitiş noktaları arasındaki uzaklıkları, arkadaşları olan diğer işçi arılarının pozisyonlarını önceden çok ince bir şekilde hesapladıklarını ortaya koyarEn usta matematikçiler bile arının hesabının kusursuzluğunu 70° 32′ (70 derece ve 32 dakika)’yı hesaplayarak ortaya koymaktadırlar Fakat bu matematik profesörlerine elinize bir cetvel alın, bu açıları tam tutturarak bir altıgen çizin desek, hele hele bu hesapları yapan üç profesöre üçünüz ayrı yerden başlayarak altıgenler çizin, ortadaki altıgenler de tam düzgün, kusursuz olsun desek hiç şüphesiz bu kadar ince bir çizimi beceremezlerdi Görülüyor ki arı, hem büyük bir teorisyendir, hem de müthiş bir pratisyendir Teoride hesaplanması çok zor olanı hesaplamış, pratikte ise bizim el ve gözlerimizle tayin edemeyeceğimiz hassaslıktaki ölçüleri tutturmuştur

Celal ÖNGÜN Teknoloji Ve Tasarım Öğretmeni